The technical name for this is the “subset sum problem”, and it’s studied by mathematicians and computer scientists as an example of a simple problem that’s very hard to actually compute. It’s actually part of a class of problems known as NP-complete, which means that, while finding an answer can be extremely difficult, it’s very quick to verify a correct answer if you have one.

Mathematics aside, this problem crops up frequently enough in real life – usually when trying to identify the components of a total that has been seen as a payment, or break up an unusual journal and figure out what elements it covers. For accountants, it’s most familiar when trying to reconcile bank payments against invoices.

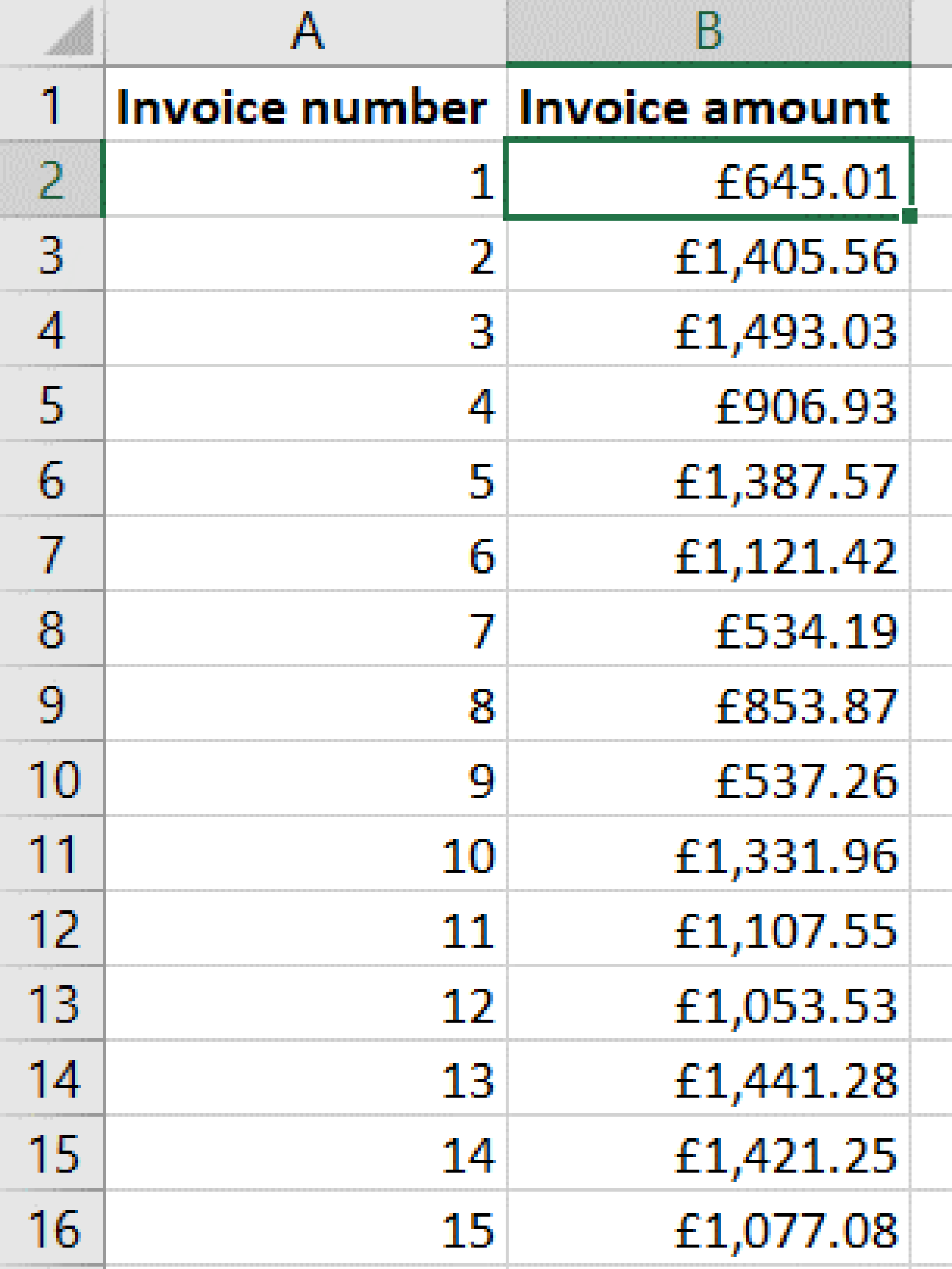
We then receive a bank payment from this customer for £7,064.54. Which invoices is this payment for? How can we identify them?

Doing this manually is not feasible – with fifteen in/out decisions to make, there are 2¹⁵ or 32,768 possibilities. A formulaic approach might work, but every invoice we add to the pile doubles the number of possibilities to check – this can become unworkable pretty quickly and is difficult right from the start. Instead, we want to automate this process using Solver.

You can read more about Solver in TOTW #257, but essentially it’s a super-charged Goal Seek add-in that comes with Excel. Once enabled from the Options menu, Solver allows you to describe an optimisation problem, and it will then solve it.

What we need to do is have Solver try adding in and taking out different combinations of items until the target is reached. The easiest way to do this is by using a 1/0 marker for each item that indicates whether it is in/excluded from the current trial solution. This is the best approach because a) calculating the total of the included items is simple with just one SUMPRODUCT function, and b) it’s straightforward to program Solver to only use 1 and 0 values in the range.

So, here’s our final setup – with a SUMPRODUCT to count the current total, a manually-entered target total, and an ABS function to calculate the exact difference between the two:

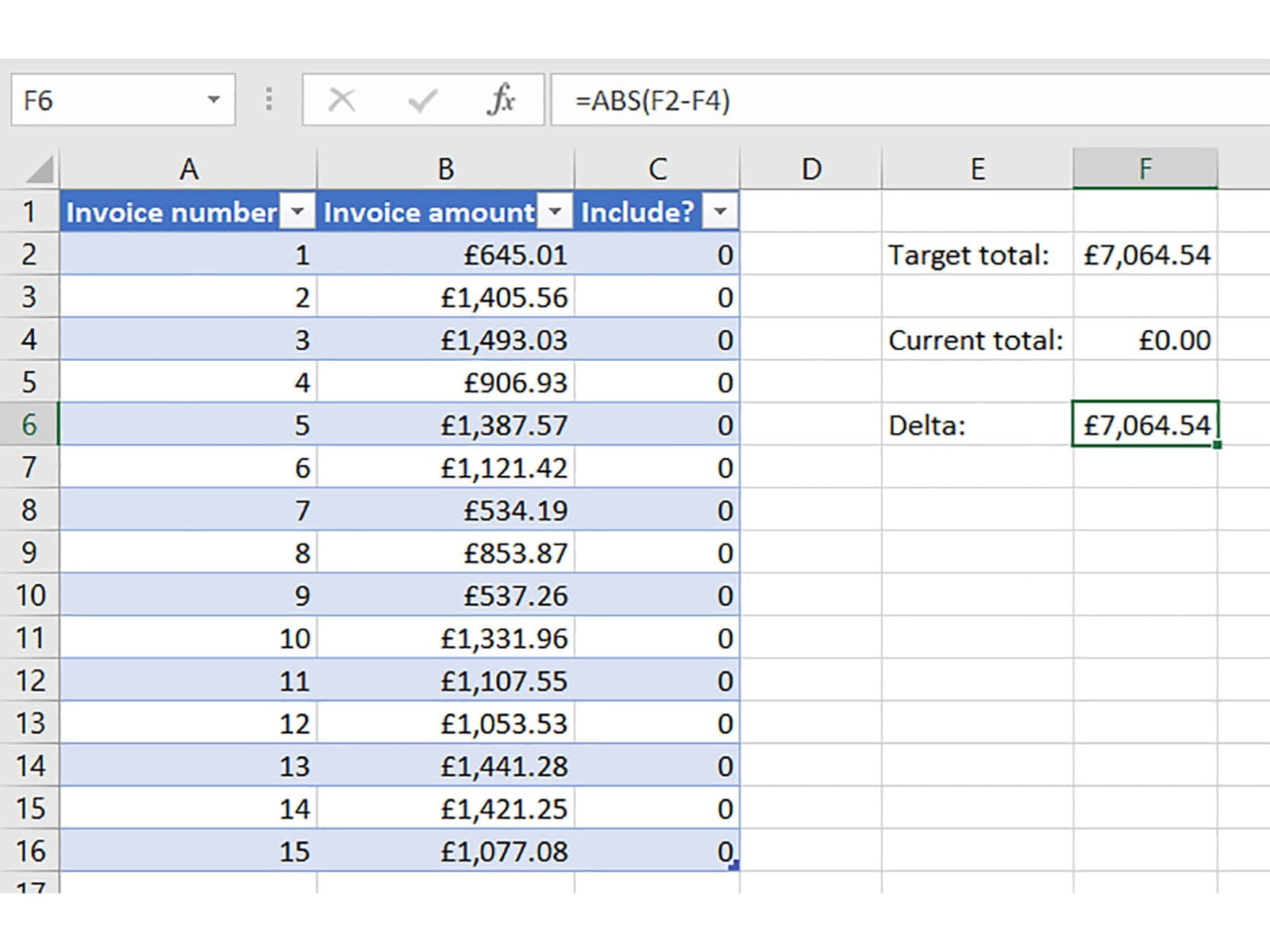
Note that we have used an Excel Table for our data – this makes the end product easily usable as a flexible template for solving problems of this type, as the SUMPRODUCT in F4 will automatically accommodate added / removed rows.

Finally, we set up our Solver Parameters:

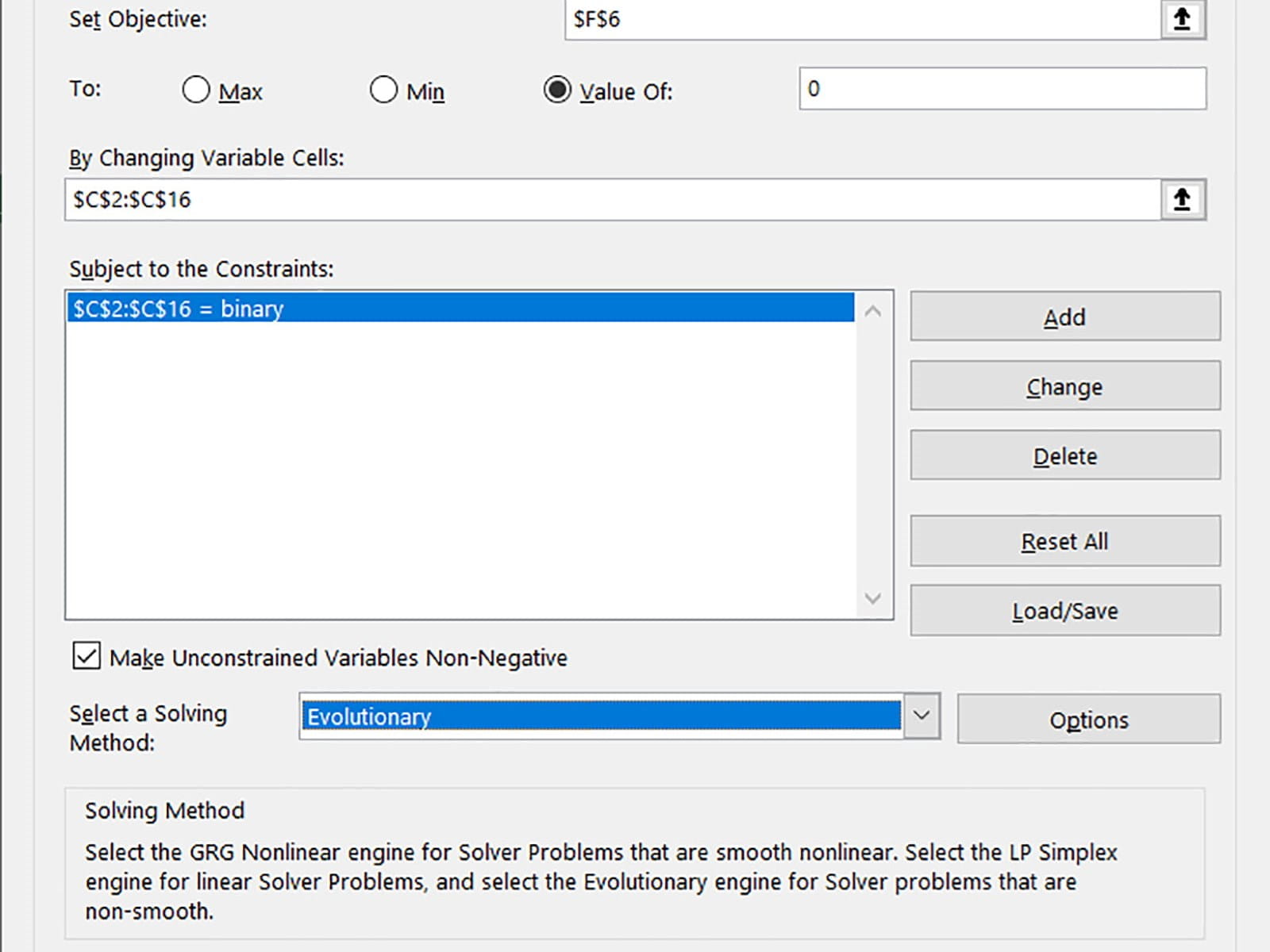
These are:

• Objective cell is set to F6, the delta calculation cell
• We want a value of 0
• Note that if we weren’t sure if a perfect solution existed, e.g. if one or more invoices had forex or rounding involved, we could instead ask for a minimal value
• The variable cells are C2:C16 – the columns of 1s and 0s showing which items are in/excluded
• We add a constraint that these cells must be “bin” – binary – i.e. enforcing that they have to be 1 or 0 only
• The solving method we have chosen is Evolutionary – the problem isn’t linear and hence this is our only option

Hit Solve and your computer will get to it.

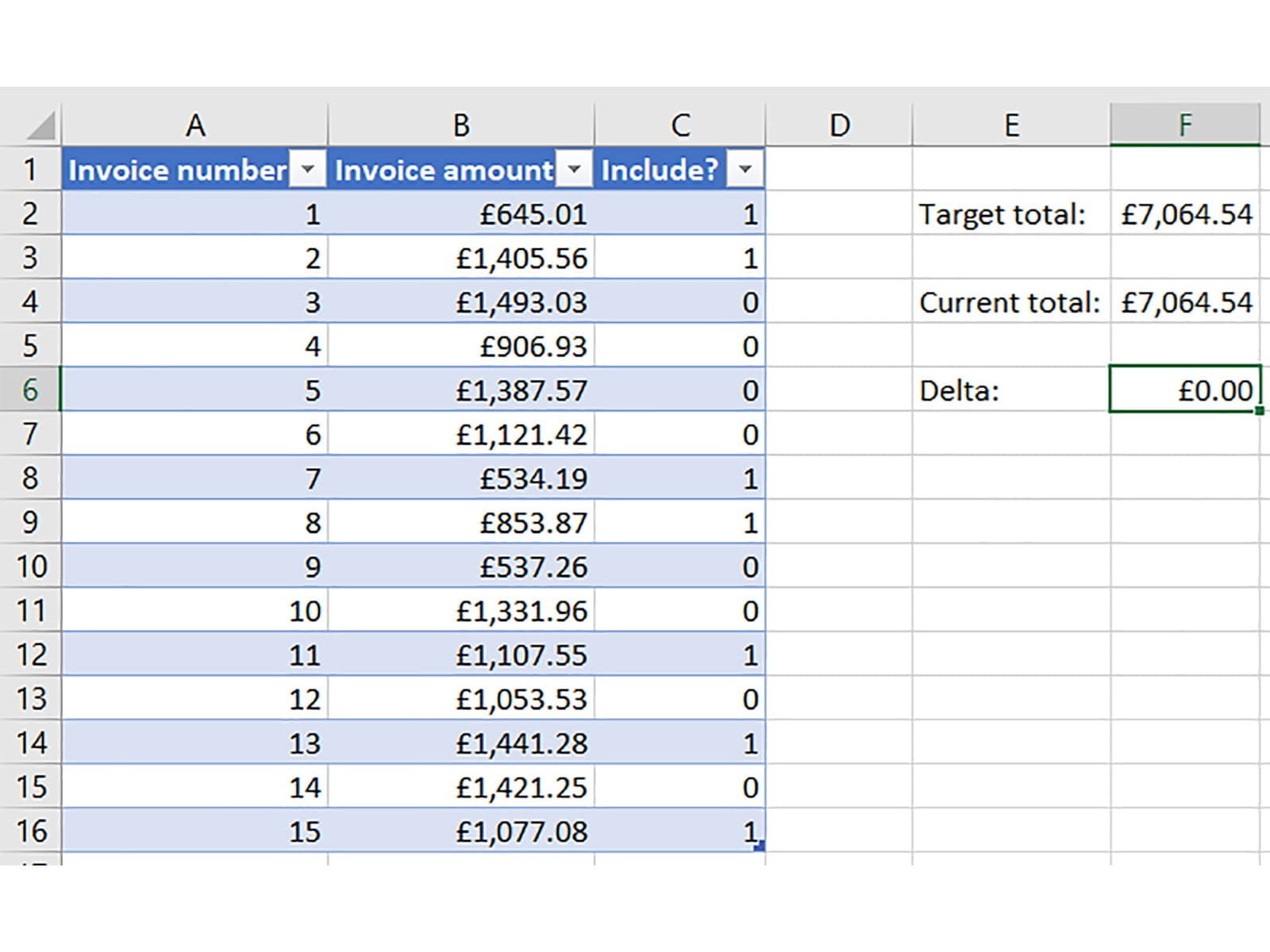
As you can see, the payment covers invoice numbers 1, 2, 7, 8, 11, 13, and 15.

This method is not foolproof. Here are a few common issues.

No solution is found

To prevent it running forever, Solver has built-in limits for how long it will search for an answer before giving up. For a problem with a large number of variables, this might well mean that there is a solution which Solver has missed – or it might mean that no solution exists and the payment includes something else you don’t know about!

You can use the Solver menu to expand the range of possible solutions that Solver checks by using the Solver Options menu and increasing the length of time that Solver is willing to wait without improving its current best attempt. However remember that there are no guarantees, especially with larger problems with more variables.

Multiple solutions exist

Especially for situations where there are many candidates, it’s likely that multiple solutions exist for some totals. In fact, if you consider the case where you have 30 invoices of ~£1,000 value, then there are about 3,000,000 possible totals (between £0.00 and £30,000.00), but 2³⁰ ≈ 1 billion combinations – so there will necessarily be many duplicated totals. Solver will stop after finding one but this may be incorrect. There’s no solution to this per se but you can bear it in mind while working.

You can try this all out for yourself by downloading the template file and giving it a go. Try finding which items add to make the total of £7,369.18.

You may also like

• Previous post - Dynamic arrays: Creating a visual work schedule
• TOTW index
• Next post – Lost coronavirus cases